Los telescopios espaciales Herschel y Planck

¿Dónde van a estar estos telescopios lanzados por la Agencia Espacial Europea?

¿Por qué se escogieron esos puntos?

Pero primero conversemos un poquito sobre la naturaleza del campo gravitatorio de un cuerpo, como el que posee el Sol, La Tierra, o la Luna (¡ y hasta usted!)

El campo gravitatorio de un cuerpo es causado por su cantidad de materia (los kilogramos de su masa) y varía con la distancia a esta (a su centro de masa) de una manera interesante, depende del inverso cuadro de la distancia.

En textos de física usted encontrará una expresión como:

para la magnitud (g) en newton/kilogramo (N/kg = m/s2) del campo gravitatorio en el exterior de un cuerpo de masa M, a una distancia r de su centro de masa.
También encontrará que es un campo vectorial, es decir, tiene magnitud y dirección. Esta dirección es radial hacia adentro (hacia el centro del cuerpo), por lo que decimos que el campo gravitatorio de un cuerpo, siempre atrae a los objetos que están a su alrededor.

Entonces, el campo gravitatorio del Sol, por ejemplo, es fuerte en su vecindario cercano y se debilita poco a poco para sitios alejados.
Podemos decir que -el campo gravitatorio no termina-, pero en realidad, a grandes distancias su contribución puede hacerse despreciable, comparada con la de cuerpos más cercanos. Así a mil veces la distancia Sol-Tierra, la intensidad de la gravedad solar es solamente una millonésima parte del valor a la distancia de la Tierra (150 millones de kilómetros).

Además, este y otros campos vectoriales satisfacen lo que llamamos el principio de superposición: cuando coexisten en un punto las contribuciones de diversos campos gravitatorios el campo neto es la suma vetorial de los aportes.

Por ejemplo, usted y yo sufrimos la influencia del campo gravitatorio de la Tierra (nos mantiene unidos a ella), de la Luna y del Sol (principales contribuyentes a las mareas) y desde luego, de los demás planetas del Sistema Solar y hasta de otras estrellas, pero se puede verificar fácilmente que estas últimas contribuciones son despreciables, con respecto a las tres primeras.

No existe pues entre la Tierra y el Sol, un punto donde el campo de la primera termine y comience el campo del segundo.
Pero si existe un punto donde el campo combinado de la Tierra y el Sol producen la fuerza centrípeta necesaria para que un tercer cuerpo de masa despreciable (un satélite artificial por ejemplo), se mantenga en una órbita circular estable y estacionaria respecto a los dos primeros. Es más existen 5 puntos, llamados Puntos de lagrange (L₁, L₂, L₃, L₄ y L5).

La justificación de los puntos L1, L2 y L3, es algo simple, ya que por estar a lo largo de la recta Tierra-Sol, los vectores de campo gravitatorio son colineales y entonces la fuerza resultante (¡suma vectorial!) apunta hacia el Sol.

Dibuje los dos vectores en cada caso sobre una copia de la figura anterior y reste los vectores de fuerza (ley de Newton de gravitación universal). Ahora solo le falta igualar esta fuerza centrípeta a su expresión cinemática (mv²/r).

Por ejemplo, para L1:

GM_sol(m)/(d_{sol-satélite})² – GM_tierra(m)/(d_{tiera-satélite})² = mv²/(d_{sol-satélite}).

Un poquito de física y matemática más y encontrará que L₁ está a 0,99 unidades astronómicas del Sol (= d_{sol-satélite}), en el lugar apropiado, a 1,5 millones de kilómetros de nuestro planeta (= d_{tierra-satélite}), para permanecer allí con un periodo orbital igual al terrestre (1 año).
En ese punto está el observatorio solar SOHO.

Trate usted de escribir la ecuación para L2 y para L3.
¿Le ve alguna ventaja particular al punto L2?
Desde luego, podemos decir que está blindado de los rayos solares por la Tierra, ya que está más allá de esta, inclusive más allá de la Luna.

En L2 está la sonda espacial Wilkinson Microwave Anisotropy Probe (WMAP) y allí irán a posicionarse los telescopios espaciales Herschel y Planck.

L₄ y L₅ requieren un poquito más de análisis vectorial y no interesan por ahora, pero acepte el reto, será divertido y aprenderá mucho.

Lo que sí es interesante aclarar es que un punto como el que nos interesa (L2) no produce una órbita totalmente estable, si se consideran las contribuciones de los demás cuerpos del Sistema Solar (Luna y el resto de los planetas). Sin embargo, este problema ya lo han resuelto los ingenieros espaciales, haciendo que los satélites se mantengan sobrevolando el punto (órbitas de Lissajous).

Referencias:

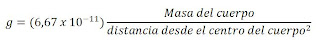
http://en.wikipedia.org/wiki/Joseph-Louis_Lagrange(http://www.freemars.org/l5/aboutl5.html)